La musica delle sfere celesti

I pitagorici furono i più ferventi fra coloro che cercarono di ordinare in forma sintetica la conoscenza. Nel quinto secolo avanti Cristo essi furono fra i primi a contemplare quella che oggi chiameremmo «matematica pura»: relazioni matematiche fini a se stesse, e non orientate a qualche applicazione pratica. Ma nonostante la loro predilezione per l'aritmetica e la geometria, i pitagorici differivano dai matematici moderni in quanta ritenevano che il significato della matematica fosse nei numeri e nelle forme geometriche, piuttosto che nelle loro relazioni. Pitagora si sentì attratto dallo studio dell'armonia musicale perché essa racchiude rapporti numerici riscontrabili anche altrove nell'Universo. Sembravano dunque emergere profondi legami fra parti della realtà altrimenti non collegate. La sua leggendaria scoperta di semplici rapporti aritmetici fra gli intervalli armonici lo persuase che dovesse esistere un legame fra matematica e musica – che la musica fosse niente di meno che il suono della matematica. 
Esiste un antico racconto, forse apocrifo, del modo in cui Pitagora scoprì illegame fra numero e armonia; Giamblico riferisce che: 

Una volta [Pitagora] stava attentamente riflettendo sulla musica, ragionando sulla possibilità di ideare qualche aiuto strumentale al senso dell'udito, per rendere sistematiche [le sue operazioni], proprio come la vista è resa precisa dal compasso, dal regolo e dalla livella, o il tatto è reso quantificabile dalla bilancia e dalle [altre] misure; mentre pensava a queste cose, gli capitò di passare accanto alla bottega di un calderaio, dove sentì i martelli battere un pezzo di ferro su un'incudine, producendo suoni che armonizzavano tutti fra loro, tranne uno. 

(a) Divisione pitagorica della sfera celeste in intervalli musicali. (b) Elaborazione medievale dell'ideale pitagorico di armonia fra umanità e ambiente, come appare in «The Tuning of the World», da Utriusque Cosmi Historia, di Robert Fludd.

Impressionato dall'armoniosa gamma di suoni prodotta dai martelli, Pitagora entrò nella bottega per scoprire come quella percussione spontanea potesse produrre suoni armoniosi. Scopri che gli intervalli musicali prodotti dai martelli erano proporzionali al rapporto dei loro pesi. Andò a casa per fare altri esperimenti, appendendo pesi diversi a corde di lunghezza regolabile, e pizzicandole per produrre suoni diversi. Scoprì che le sequenze di note musicali più piacevoli erano legate da semplici rapporti aritmetici di numeri interi, rapporti per i quali lui e i suoi seguaci nutrivano un profondo rispetto. Come pure veneravano il legame fra i numeri e la musica forgiata nella bottega del calderaio – un legame numerologico. 

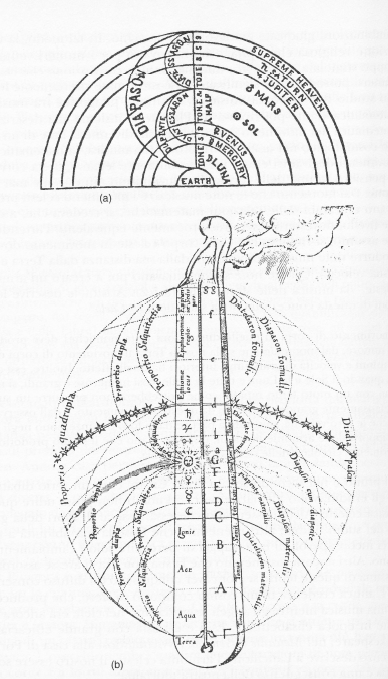
A Pitagora è attribuito il merito di aver scoperto che pizzicando corde fra le cui lunghezze esistano rapporti particolari è possibile produrre note in relazione armoniosa. Quanta più corta è la corda, tanto più alta è la nota. Dimezzando una corda vibrante si ottiene una nota più alta di un'ottava; raddoppiandola si ottiene una nota più bassa di un'ottava. L'orecchio sembra gradire le combinazioni di note prodotte da corde fra le cui lunghezze esistano i seguenti rapporti: 1:1, 1:2, 2:3 (la «quinta» perfetta), o 3:4. Se si considera un rapporto come 7:11, il risultato è notevolmente dissonante. Pitagora riuscì a determinare i rapporti fra le lunghezze delle corde necessari per produrre combinazioni giudicate gradevoli dall'orecchio. In tal modo, la venerazione religiosa che i pitagorici nutrivano per i numeri venne fin troppo stimolata, e per circa duemila anni la convinzione che ciascun numero possedesse un significato nascosto rimase strettamente legata allo studio dell'armonia musicale. L'unione pitagorica fra musica e matematica venne poi ripresa da Platone e, insieme alla descrizione matematica dei movimenti dei corpi celesti, divenne la base di un quadro cosmologico nel quale le armonie della musica, la matematica e i movimenti degli astri erano inestricabilmente legati. Questa corrente di pensiero fu una delle forme di riduzionismo più estreme mai concepite. Dal momento che le note musicali e i movimenti celesti presentavano entrambi delle relazioni matematiche, si credeva che, a qualche livello, dovessero essere reciprocamente equivalenti. Partendo da tale assunto, si riteneva che ogni corpo celeste in movimento dovesse produrre note musicali dipendenti dalla sua distanza dalla Terra e dalla sua velocità. Queste note si combinavano poi a creare un'armonia celeste: «la musica delle sfere» (v. Figura). Aristotele descrive le ragioni di questa concezione nella sua opera De Caelo: 

il movimento di corpi di quelle dimensioni [astronomiche] deve produrre un rumore, dal momento che sulla nostra Terra il movimento di corpi di dimensioni e velocità di gran lunga inferiori ha quell'effetto. Inoltre, essi dicono, quando il Sole e la Luna e tutte le stelle, così numerose e grandi, si muovono con un moto tanto rapido, come potrebbero non produrre un suono immensamente grande? Partendo da questo ragionamento, e dall'osservazione che le loro velocità, misurate a partire dalle loro distanze, sono negli stessi rapporti delle armonie musicali, essi affermano che il suono prodotto dal movimento circolare delle stelle sia un'armonia. 

Nel primo e nel secondo secolo dopo Cristo, ci fu un serio dibattito, fra gli eruditi, volto a chiarire perché l'uomo non possa udire questa musica celeste. Alcuni asserivano che essa fosse al di fuori della gamma dei suoni udibili; altri ritenevano che fosse la sua ubiquità a renderci inconsapevoli di essa, capaci di percepire solo i cambiamenti di suono. Altri ancora sostenevano che la sua potenza ci avesse assordato. Nessuna di queste teorie sembra aver conquistato un diffuso consenso. 
L'antica credenza di un cosmo composto di sfere, che producevano una musica mentre gli angeli le guidavano nei cieli, era ancora fiorente in epoca elisabettiana. Essa è esposta con grande efficacia da Shakespeare, nel Mercante di Venezia. Avvicinandosi alla casa di Porzia, Lorenzo descrive a Lancillotto l'armonia celeste; il nostro essere sordi a essa è una conseguenza della nostra mortalità: 

Vedi la luna come dolcemente dorme su questa aiuola; noi, lì seduti, lasceremo insinuarsi per le orecchie al cuore il filtro della musica. Il soffice silenzio della notte si intona con gli accenti della dolce armonia. Siedi, Gessica, guarda come il pavimento del cielo è tutto costellato di stateri d'oro scintillanti; e neanche uno, neanche il più piccino, di questi globi, che non percorra l'orbita sua cantando come un angelo in coro coi cherubini occhi novelli. E la stessa armonia è anche nelle anime nostre immortali; ma finché sono chiuse in questi nostri rozzi cofani d'argilla, non le possiamo sentire.

Nella teoria musicale pitagorica c'era molto di più dell'armonia celeste. Oltre alla musica delle sfere celesti (musica mundana) venivano distinte altre due varietà di musica: il suono degli strumenti, come i flauti e l'arpa (musica instrumentalis) e la musica continua e non udibile emanata dal corpo umano (musica humana), che scaturisce da una risonanza fra il corpo e l'anima. L'assunto importante alla base di queste distinzioni, che venne ripreso da Platone e che poi influenza tanto a lungo la filosofia occidentale, è che la musica celeste esiste con le sue proprietà in modo assolutamente indipendente dall'ascoltatore umano. Secondo Platone, ciò che noi udiamo dell'armonia musicale è un pallido riflesso di una perfezione più profonda esistente nel mondo dei numeri, perfezione che fa mostra di sé nei movimenti planetari. Noi l'apprezziamo solo perché i ritmi del nostro corpo e della nostra anima sono predeterminati in modo da risuonare con l'armonia del regno celeste. Platone rinforzò questa filosofia trascendentale della musica inquadrandola nella sua concezione filosofica più ampia, in cui il mondo delle apparenze era l'ombra di un altro mondo perfetto, contenente le forme ideali delle cose intorno a noi. In ultima analisi, la filosofia di Platone è la fonte della filosofia assolutista della musica, che abbiamo discusso prima. 

Nel mondo medievale, lo status della musica ci viene rivelato dalla sua presenza, accanto all'aritmetica, alla geometria e all'astronomia, nel Quadrivium – il programma di istruzione articolato in quattro discipline. Gli studiosi medievali di musica si consideravano alla stregua di scienziati, e la relazione della musica con la matematica e l'astronomia era ritenuta il suo aspetto più importante. Prima degli studi di Boezio, nel nono secolo, l'idea di armonia musicale non venne considerata indipendentemente dagli argomenti più ampi dell'armonia etica o celeste. Un grande cambiamento nel modo di concepire la musica poté avvenire solo in un nuovo clima, che abbandonasse la sua totale sottomissione alle autorità del passato e cercasse di rispondere agli interrogativi osservando o ascoltando la realtà, e non semplicemente limitandosi a leggere di essa.