«“Sapete che cos’è un matematico?”, chiedeva il celebre fisico Lord Kelvin ai suoi studenti. E dopo aver scritto alla lavagna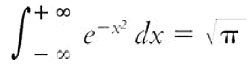 
spiegava: “Un matematico è un uomo per il quale questa cosa è tanto evidente quanto 2+2=4 per voi”». Questo è solo uno dei numerosi e gustosi aneddoti che si possono trovare nel classico libro di Eric Temple Bell (1883-1960), matematico scozzese che insegnò prima all’Università di Washington e poi al Caltech di Los Angeles, scopritore delle serie di potenze che portano il suo nome e che vengono utilizzate per studiare le proprietà delle funzioni aritmetiche moltiplicative e vincitore, nel 1924, del Bôcher Memorial Prize dell’American Mathematical Society. Le pagine di Bell conducono il lettore attraverso l’intera storia della matematica, da Archimede a Poincaré, disegnando uno dopo l’altro il profilo degli uomini che le hanno dato i maggiori contributi. Così scopriamo che Descartes desiderava “unicamente la tranquillità e il riposo”, ma che “fu troppo spesso ridotto a trovarli negli accampamenti”, che Fermat aveva scoperto “una dimostrazione veramente bella” di un importante teorema, ma che non la poteva scrivere perché il “margine è troppo piccolo” (dando così origine ad uno dei rompicapi più famosi della storia della matematica) e che “Newton non ha avuto maestri né uguali, per la facilità con cui poteva concentrare tutte le forze del suo intelletto su una improvvisa difficoltà”. Impariamo anche che “Eulero calcolava senza sforzo apparente, come gli uomini respirano”, che Napoleone Bonaparte definì Lagrange come “l’alta piramide delle scienza matematiche” e che Gauss, “il re dei matematici”, ebbe origini tutt’altro che regali. Se Leibniz rappresenta un’eccezione al proverbio “Chi troppo abbraccia, nulla stringe”, dal momento che, oltre che alla matematica, “il suo splendido genio” apportò contributi significativi a “diritto, religione, politica, storia, letteratura, logica, metafisica, filosofia speculativa”, dalla famiglia Bernouilli, “che, nel corso di tre generazioni, ha dato otto matematici, di cui diversi eminenti”, troviamo conferma all’opinione secondo cui “soltanto la natura, e non l’ambiente è il fattore determinante del genio”. Incontriamo anche personaggi la cui genialità è emersa in condizioni avverse, come Abel, nato nello sperduto paesino di Findoe, in Norvegia, e che “ha lasciato ai matematici da lavorare per cinquecento anni”, o Galois, che la notte prima di venire ucciso in un duello alla pistola a soli ventun’anni, scrive un lavoro fondamentale sulla solubilità delle equazioni per mezzo di radicali, interrompendosi di tanto in tanto “per scarabocchiare in margine: Mi manca il tempo! Mi manca il tempo!”, o ancora Hermite, che fu ammesso alla Scuola Politecnica “sessantottesimo in graduatoria, benché fosse già superiore, come matematico, ai suoi esaminatori”. Dalla vita di Weierstrass, “il padre dell’analisi moderna”, e di Boole, “lo scopritore della matematica pura”, impariamo che “è possibile per un uomo darsi per molto tempo all’insegnamento elementare pur mantenendo la propria attività matematica”, mentre Riemann, “i cui lavori basterebbero appena a riempire un volume in ottavo”, ci insegna che la qualità è più importante della quantità, dato che “ha rivoluzionato dal più al meno tutto ciò che ha trattato”. Con Poincaré, “l’ultimo scienziato che abbracciò praticamente tutto il dominio della matematica, pura e applicata”, si chiude un libro che, oltre alla vita dei protagonisti, espone anche in modo sintetico e sufficientemente comprensibile le rispettive scoperte e ne illustra l’impatto e i riflessi sul complesso delle conoscenze matematiche precedenti e successive.