Nella ricerca della verità di un fenomeno, raccogliere informazioni è il primo passo per costruire una solida conoscenza. Innanzi a fenomeni vasti e complessi, le informazioni che si possono raccogliere possono essere molto numerose, eterogenee fra loro, complesse, disorientando il ricercatore nel suo cammino di conoscenza. La statistica è una scienza che fornisce gli strumenti per governare questo caos informativo, permettendo di poter dare descrizione, attraverso una necessaria riduzione, e di poter trarre conclusioni valide ed utili.
Oggi viviamo immersi in una Infosfera (secondo l’espressione del filosofo Luciano Floridi) in cui in ogni secondo miliardi di dati legati alle attività umane e naturali sono prodotti e collezionati. Il dato e la statistica sono ubiqui e si ha la credenza che siano in grado di dare qualsiasi tipo di risposta e soddisfare ogni esigenza dell’umanità. Lo sviluppo dell’informatica e dell’intelligenza artificiale, sostenuti dalla statistica, hanno aperto la strada a mezzi “intelligenti” in grado di aiutare l’uomo, se non addirittura sostituirlo, in alcuni compiti quotidiani.
È interessante osservare come l’attività umana sia stata accompagnata, sin dagli albori, dalla necessità di controllo e di governo, anche tramite la misurazione e il censimento delle risorse disponibili. Già in epoca preistorica abbiamo prova di oggetti incisi con tacche atte a contare; migliaia di anni dopo, nella Bibbia abbiamo testimonianza di differenti attività di censimento. L’interesse e la consapevolezza dell’importanza dei censimenti sono cresciuti col tempo: il Concilio di Trento del 1563 introdusse i registri parrocchiali per raccogliere le informazioni delle nascite, dei matrimoni e dei decessi.
Grazie alla disponibilità di queste informazioni, nel 1600 nasce la statistica, intesa all’origine come “aritmetica politica”, cioè come “l’arte di ragionare mediante le cifre sulle cose che riguardano il governo” (William Petty), con i primi esempi di statistica demografica già di un certo interesse: numerosità della popolazione di Londra, rapporto maschi/femmine nelle nascite, distinzione tra popolazione urbana e rurale. Si è concretizzata successivamente un'attenzione verso gli aspetti più disparati della vita, dalla stima di mortalità alla descrizione delle cose dello Stato (da cui anche il termine di statistica).
Successivamente, alla descrizione dei dati comincia ad essere associata una valutazione probabilistica (soprattutto in riferimento alla durata della vita) al cui sviluppo ha contribuito nell’Ottocento la divulgazione dei concetti di “variabilità biologica” e di "uomo medio".
Dal XX secolo si assiste a un fiorire di teorie e tecniche fondamentali per l'analisi e il confronto tra gruppi di dati in associazione a criteri di generalizzazione dei risultati. La velocità di calcolo raggiunta con l'introduzione del computer, essenziale per l'elaborazione di grandi masse di dati, ha contribuito in modo determinante allo sviluppo della statistica attuale.
Oggi i metodi statistici sono applicati ad ogni aspetto della conoscenza umana: biologia, economia, fisica, medicina, chimica, lettere, arti, processi industriali, sport, scienze sociali e comportamentali, archeologia. Questo perché sono un ottimo strumento per approfondire e migliorare la conoscenza di un fenomeno attraverso un procedimento metodologicamente corretto e riproducibile. Nel linguaggio comune numerosi aspetti di vita quotidiana vengono riproposti in veste statistica, anche se spesso in modo improprio, per esempio quando confondiamo dato e informazione.
Il “dato” è un termine ormai utilizzato quotidianamente nei mezzi di comunicazione di massa e nel dialogo abituale e come suo sinonimo spesso viene utilizzato il termine “informazione”. Dal punto di vista della teoria dell’informazione, questi due termini non sono sinonimi, ma sono relazionati da una Definizione Generale d’Informazione (GDI): i dati dovranno essere interpretati o manipolati per diventare informazione. Il dato, o variabile, è definibile come una rappresentazione oggettiva, non interpretata e limitata della realtà del fenomeno di interesse. Esiste un legame delicato fra il dato e l’informazione da esso veicolata. Il meccanismo per trarre informazione dai dati deve seguire un metodo di ricerca scientifico, grazie all’analisi statistica il dato si arricchisce di significato.
La ricerca statistica si caratterizza per la sistematicità del processo d’indagine e per la riproducibilità del metodo adottato. I principali approcci al processo d’indagine statistico sono: descrittivo, comparativo, speculativo.
Nel caso di studi comparativi o speculativi, le tappe principali del percorso di ricerca sono: la definizione degli obiettivi (ossia scegliere quale criterio possa spiegare una differenza tra due o più gruppi), l’individuazione del metodo di campionamento dei membri dei gruppi, l’individuazione di quali variabili studiare, la scelta del modello probabilistico più adatto a descrivere il fenomeno, la raccolta dei dati e la loro elaborazione, l’interpretazione dei risultati ottenuti e la loro comunicazione.
Il campionamento è necessario in quanto non è mai possibile raccogliere le informazioni di tutta la popolazione d’interesse in quanto si è vincolati da risorse limitate. Questo approccio introduce un’incertezza, ponderata, dovuta al fatto che le proprietà del campione estratto non sono uguali a quelle della popolazione da cui proviene. È quindi necessario introdurre un livello di incertezza, rappresentato dal P-Value, nelle conclusioni che si possono raggiungere.
L’approccio statistico richiede nuovi modi di pensare e di indagare: la scelta di un buon campione utilizzando una tecnica che non introduca errori, la selezione dei dati da raccogliere, come rappresentare e divulgare i risultati. Dietro ciascuno di questi passaggi possono nascondersi imprevisti capaci di annullare il valore del risultato ottenuto. Fondamentale è determinare quale test probabilistico sia più appropriato per la verifica delle ipotesi, ossia il razionale che giustifichi lo studio.
Il confronto tra campioni appartenenti a gruppi con caratteristiche differenti (ad esempio in ambito medico la risposta di soggetti trattati con una certa terapia rispetto a quelli trattati con una terapia differente) implica la verifica di un’ipotesi di base espressa come: “nessuna differenza statistica esiste tra i parametri dei gruppi e le eventuali differenze riscontrate sono giustificate dalla variabilità casuale dovuta a come sono stati selezionati i soggetti e raccolti i dati”. Tale ipotesi, che si definisce ipotesi zero, fa riferimento alla “popolazione” e non ai campioni da essa estratti, in quanto non siamo interessati ai campioni statistici di per sé ma ai risultati del loro confronto. Se è valida l’ipotesi zero i campioni non risultano differenziati e, fino a prova contraria, fanno parte della stessa popolazione per quanto riguarda il carattere esaminato.
Per quanto sembri assurdo, il processo di verifica di un’ipotesi si sviluppa correttamente rifiutandola quando si riscontrano i presupposti per non avvallarla. Il rifiuto dell’ipotesi zero permette di prendere in considerazione l’ipotesi alternativa, che sostiene l’esistenza di una differenza non casuale per il carattere esaminato tra i due gruppi confrontati.
Il processo di rifiuto dell’ipotesi zero viene accompagnato da un livello di probabilità di commettere un errore nel rifiutare l’ipotesi, detto P-Value. Ottenere dai test statistici un P-Value significativo è la condizione necessaria per poter veder riconosciuto dalla comunità scientifica il proprio lavoro e vederlo pubblicato. Tale “affanno” ha portato a coniare nel tempo la celebre frase “torturando i dati a sufficienza, si può far dire loro quello che si vuole”, facendo cadere dubbi sulla “sicurezza” di usare una soglia di significatività come garanzia della veridicità e riproducibilità del lavoro pubblicato, criteri fondamentali della ricerca scientifica.
Molti libri e intere sezioni di riviste si sono occupate di formare i fruitori dei lavori scientifici al fine di renderli consapevoli di questi rischi. La non riproducibilità di un risultato scientifico si traduce nell’impossibilità da parte di un ricercatore di riprodurre, e quindi confermare, i risultati pubblicati da un collega.
Dietro questa difficoltà a riprodurre i risultati, senza cadere in dubbi legati a voler pubblicare risultati per opportunità economica o di prestigio, si cela la scelta di non esplicitare del tutto i metodi e passaggi che descrivono l’esperimento svolto come la scelta di una popolazione particolare rispetto ad una campionata casualmente o la non dichiarazione di tutti i passaggi d’elaborazione e pulizia dei dati.
Per porre rimedio a questo aspetto oggi sempre più riviste incoraggiano ad alcune pratiche come la condivisione del set di dati con i revisori e con i lettori della rivista, la condivisione del codice statistico utilizzato per elaborare i dati e la definizione di altri parametri statistici (come la potenza o il rischio di falso positivo).
Sicuramente il problema della riproducibilità dell’esperimento è rilevante per chi fa ricerca. Il lettore o lo studente devono avere a mente questo aspetto per sviluppare un corretto senso critico.
Quanto esposto non deve screditare il valore della pubblicazione scientifica e il lavoro dei ricercatori, degli editori e dei revisori delle riviste scientifiche. Per affrontare la lettura di un articolo di ricerca nell’ambito della statistica è consigliabile seguire alcuni comportamenti utili a non travisare i risultati.
Il primo aspetto da considerare, in caso si tratti di leggere un lavoro che citi altri studi, è la necessità di verificare i documenti originali per capire se quanto riportato rispetti il messaggio degli autori e per verificare se i risultati siano stati interpretati in maniera parziale.
Un aspetto importante da considerare è la numerosità del campione in esame. Al crescere della numerosità di un campione aumentano le risorse e le capacità necessarie per raccogliere, analizzare ed elaborare i risultati. Un autore deve bilanciare le proprie esigenze di ricerca con le risorse (limitate) a disposizione. Un fenomeno che si osserva quando i campioni in esame sono “piccoli”, o sono formati selezionando i casi più “estremi”, è la “regressione verso la media”. Il primo a documentarla è stato Galton, nel 1800. Tutte le misurazioni sono composte da una parte vera e una parte di errore casuale. Quando le misurazioni effettuate portano a risultati “estremi” è probabile che siano in parte causati dal caso più che dal fenomeno di interesse, se si ripetesse infatti l’esperimento sarebbe altamente probabile osservare risultati meno estremi. Minore è la numerosità del campione, maggiore è la possibilità di osservare questo fenomeno.
La rappresentazione grafica dei risultati è un’alternativa efficace per spiegare e raccontare i risultati. I grafici possono essere strumenti di ragionamento o di razionalizzazione. Il messaggio trasmesso dai grafici corre il rischio di venire distorto per essere adattato alla visione del lettore o dell’autore, piuttosto che riflettere sul vero messaggio. L’uso di colori, di scale non appropriate può falsare le vere proporzioni dei fenomeni analizzati, facendo facilmente confondere il lettore. Il meccanismo di difesa che si può utilizzare è quello di ragionare sui numeri, cercando di valutare se le proporzioni raffigurate rispecchino davvero i valori indicati o cercando di capire se i dati mostrati, utilizzando altre fonti d’informazione, seguano davvero questi andamenti.
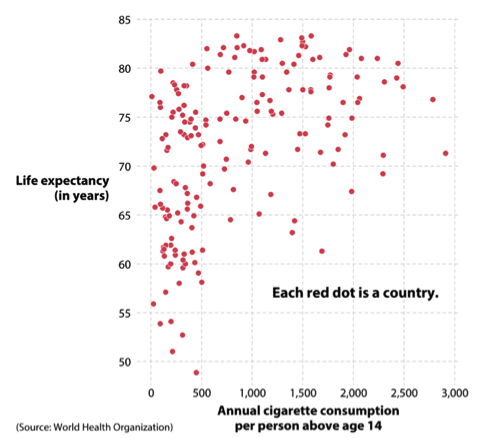Il grafico qui riportato, che visualizza il consumo annuo nazionale medio di sigarette per individuo rispetto all’aspettativa di vita media nazionale, dati della World Health Organization, porterebbe spontaneamente a dire che il crescere del consumo di sigarette sia correlato con un aumento positivo dell’aspettativa di vita media. Questo potrebbe poi essere corroborato dall’analisi statistica di regressione sui dati, che infatti mostrerebbe una correlazione positiva e statisticamente significativa tra l’incremento del numero di sigarette consumate e l’aumento dell’aspettativa di vita. Tale risultato sarebbe paradossale ed andrebbe contro ogni convinzione fin qui avuta sul rapporto tra il fumo e la salute.
Il tranello di questo grafico, che introduce anche il problema che la correlazione non implica la causalità, deriva dal fatto che il grafico rappresenta insieme tutte le nazioni del mondo, senza dividerle per ricchezza pro capite. In questo modo si mescolerebbe l’effetto dell’alta mortalità, a prescindere dalle cause, presente nei paesi più poveri e la maggior aspettativa di vita per i cittadini dei paesi più ricchi, a prescindere delle patologie e dei comportamenti. In questo modo, la presenza di una “variabile nascosta”, e non rappresentata nel grafico, come la ricchezza pro capite media permette di generare un risultato formalmente statisticamente valido, ma erroneo. Quindi una correlazione fra due variabili dovrebbe essere considerata come punto di partenza per un’analisi scientifica corretta, non come punto di arrivo.
Se questi dati fossero stati utilizzati per produrre un lavoro scientifico, statisticamente formalmente valido, si potrebbe biasimare quindi l’autore di non aver compiuto le accurate analisi sui dati a disposizione, traendone conclusioni affrettate. Ci troveremmo davanti a errori sia metodologici, ignorare la variabile nascosta della ricchezza pro capite e quindi valutando erronee correlazioni, sia di campionamento, utilizzando i dati in proprio possesso male considerando equivalenti nazioni con profonde differenze economiche, sociali e politiche.
Il valore di un ricercatore, e di conseguenza del suo lavoro, è non solo la capacità di scoprire aspetti nuovi ma soprattutto, dopo aver ottenuto un risultato, avere il senso critico di rimetterlo in discussione, analizzandolo da altri punti di vista in modo da poter rafforzare le proprie convinzioni e risultati.
Il lettore invece, in questo frangente particolare, dovrebbe attenersi a due principi; da un lato sostenersi con quanto oggi è già di dominio pubblico, ossia il rapporto negativo fra fumo e salute, e dall’altro leggere nel grafico solo quanto esso rappresenta evitando di andare oltre la mera raffigurazione delle variabili.
Siamo immersi in un universo affascinante ma complesso, la statistica è oggi una scienza molto importante perché aumenta la capacità umana di “contare” e abilita l’uomo a fare inferenza permettendo di trarre indicazioni su fenomeni vasti, non osservabili o ponderabili direttamente. Di fronte al rischio di trovarsi innanzi ad errori e distorsioni, ripropongo le confortanti parole di John Henry Newman [1]:
“Ciò che vorrei sollecitare in ognuno, qualunque possa essere la sua particolare linea di ricerca, – ciò che vorrei sollecitare negli uomini di scienza nei loro pensieri di teologia, – ciò che mi arrischierei di raccomandare ai teologi, quando la loro attenzione è attirata dall'oggetto di indagini scientifiche, – è una grande e ferma credenza nella sovranità della verità. L'errore può fiorire per un momento, ma alla fine prevarrà la verità”.
[1] J. H. Newman, Argomenti universitari. Discorso VIII, 1855.