Presentazione e commento dello studio di
R. Rashed, Le modèle de la sphère transparente et l’explication de l’arc-en-ciel: Ibn al-Haytham, al-Fārisī (1970)
1. Introduzione allo studio di Roshdi Rashed
I personaggi
Prima di addentrarci nel vivo della materia, presentiamo brevemente i personaggi che ci accompagneranno nel corso di questo breve viaggio alla scoperta delle teorie dell’arcobaleno di due pensatori musulmani Ibn al-Haytham e Al-Fārisī, rispettivamente del X e del XIII secolo, così come presentate Roshdi Rashed, in un suo studio del 1970.
Ibn al-Haytham, conosciuto spesso come Alhazen o Alhacen, è nato a Bassora nel 965 e morto al Cairo nel 1039. Matematico, filosofo e fisico del mondo medioevale arabo-musulmano, è tra i primi promotori del metodo scientifico sperimentale, nonché uno dei primi fisici teorici a utilizzare la matematica. Diventa celebre per i suoi lavori pionieristici nei campi dell’ottica fisiologica e dell’ottica geometrica. Alcuni, a ragione, lo hanno descritto come il primo vero scienziato.
Al-Fārisī, nato nel 1267 nell’attuale Iran, precisamente a Tabriz, e morto nel 1320, è un fisico, matematico e scienziato musulmano persiano. A lui si devono due importanti contributi alla scienza, uno sull’ottica e l’altro sulla teoria dei numeri. È l’autore del Tanqīḥ Kitāb al-Manāẓir (La revisione del trattato sull’ottica di Ibn al-Haytham).
Roshdi Rashed nato al Cairo nel 1936 è un matematico, filosofo e storico delle scienze, la cui opera si concentra in particolare sulle scienze matematiche e sulla fisica del mondo arabo medioevale. Essendo uno dei primi storici a studiare approfonditamente i testi antichi e medioevali arabi, i loro percorsi attraverso le scuole e i corsi orientali, e il loro immenso apporto al progresso delle scienze occidentali, in particolare per quanto concerne l’algebra e le prime formalizzazioni della fisica, il suo lavoro ha quindi il merito di esplorare e spiegare il pensiero arabo troppo spesso sconosciuto e trascurato dal mondo occidentale.
Il tema
La scelta di proporre a distanza di anni lo studio di Roshdi Rashed del 1970: Le modèle de la sphère transparente et l’explication de l’arc-en-ciel: Ibn al-Haytham, al-Fārisī ‘Il modello della sfera trasparente e la spiegazione dell’arcobaleno: Ibn al-Haytham, al-Fārisī’, trova giustificazione nella presenza di tesi di notevole interesse, ai fini della valutazione storica degli studi, svolti nel corso dei secoli, sul fenomeno dell’arcobaleno e sulla centralità che, a tal proposito, ha assunto la riforma dell’ottica di Ibn al-Haytham.
Nel suo articolo, infatti, Rashed sostiene che questi tentativi intrapresi per spiegare l’arcobaleno debbano essere considerati come espressioni circoscritte e non chiavi di lettura per comprendere e valutare il progresso della scienza dei fenomeni luminosi. Sin da Aristotele l’argomento è presentato in maniera del tutto particolare e indipendente dall’ottica, tanto che persino Ibn al-Haytham, nonostante l’intenzione di applicarvi il composito metodo di norme matematiche e sperimentali, da lui stesso messo a punto nella riforma dell’ottica, rimarrà imbrigliato nella trattazione tradizionale e quindi geometrica del fenomeno, rinunciando all’approccio sperimentale. D’altro canto, se è un’evidenza storica che nel XIV secolo, al-Fārisī e Theodoric, indipendentemente l’uno dall’altro, intraprendono uno studio indiretto e quindi sperimentale sull’arcobaleno, solo in seguito alla riforma dell’ottica di Ibn al-Haytham e contro, almeno per quanto concerne al-Fārisī, la sua spiegazione decisamente riduttiva del fenomeno, Rashed nel corso dell’articolo tenta di dimostrare anche la necessità logica della consequenzialità di questi eventi, giungendo alla occlusione che: «Concepita e realizzata per integrare lo studio di un fenomeno così complesso, come l’arcobaleno, nella nuova ottica, la costruzione del modello della sfera [di al-Fārisī] fu non solo sollecitata da questa ottica, ma quest’ultima fu, di gran lunga, la condizione del suo avvento». (trad. di Rashed, 1970, p. 139)
Rinviando alla lettura integrale dell’articolo per maggiori approfondimenti, ci limitiamo a riportarne, qui di seguito, la traduzione della seconda parte, attraverso la quale viene esposta la spiegazione dell’arcobaleno di Ibn al-Haytham, per poi riassumere brevemente la critica e la proposta di al-Fārisī, così come la presenta Rashed nella terza parte.
2. Il modello della sfera trasparente e la spiegazione dell’arcobaleno: Ibn al-Haytham, al-Fārisī
[Traduzione dal francese all’italiano delle pp. 116-120 di: Rashed R., 1970, “Le modèle de la sphère transparente et l’explication de l’arc-en-ciel: Ibn al-Haytham, al-Fārisī,” Revue d’Histoire des Sciences, 23, p. 109-140. Le note a piè di pagina, riportate di seguito, sono frutto della traduzione di quelle presenti nel testo di Rashed.]
Ibn al-Haytham affronta l’esame dell’arcobaleno nella ferma intenzione di applicarvi il progetto che aveva sperimentato con successo in altre ricerche riguardanti l’ottica[1]: la fusione delle scienze matematiche con la fisica. Egli non tarda, infatti, a dichiarare:
Nell’aria densa, si incontrano sempre due fenomeni (l’alone e l’arcobaleno), formati da una forma necessaria allo stesso ordine; l’alone ha sempre la forma di un cerchio finché non è colpito da un accidente che lo modifica e l’arcobaleno ha sempre la forma di una porzione di cerchio. Poiché il loro oggetto è l’aria, è necessario considerarli da un punto di vista fisico e poiché la loro figura è circolare, è necessario considerarlo anche da un punto di vista matematico. È per questo che lo studio che permette di ricercare la verità di questi due fenomeni si compone di fisica e matematica. Ne parleremo in un saggio che ne ricerca la verità secondo esigenze legate tanto a questioni fisiche che a principi matematici e tenendo conto di ciò che è conforme alla loro realtà»[2].
D’altronde, sappiamo già che questa fisica, per spiegare la forma dell’arco, propone che la luce riflette sulle nuvole prima di giungere all’occhio e conferma, in una rappresentazione del cosmo, che le parti di quest’ultimo che circondano gli elementi —aria o acqua, ad esempio— presentano una forma sferica. L’aria umida e densa si muove nell’atmosfera da una superficie sferica a un’altra della medesima forma e questo elemento può avere unicamente la forma sferica, poiché il centro di questa sfera è lo stesso dell’universo. Il cammino della fusione tra matematica e fisica è già tracciato: lo studio dell’arco può essere considerato come quello della luce su una porzione di sfera riflettente. Bisogna però ancora assicurarsi che l’aria umida e densa possa essere assimilata a una superficie riflettente. Ibn al-Haytham scrive:
«Non si può vedere nulla del colore di un oggetto apparso su delle superfici che non sono uniformi e se si riesce a vedere qualcosa si tratta di un qualcosa di estremamente attenuato e flebile. È quindi necessario che il corpo umido dove il raggio può riflettersi e dove il colore dell’oggetto considerato può apparire abbia una superficie liscia e composta da parti lisce che non siano infinitamente piccole; più la superficie è uniforme e più le parti che la compongono sono grandi, più ciò che appare su di essa ha un’immagine netta e un colore limpido; di contro, meno la superficie è liscia e più le parti che la compongono sono piccole, più ciò che appare su di essa è sfocata e il colore attenuato. Così i due fenomeni che abbiamo sopra citato si possono trovare solo nell’aria umida, se questa ha una forma che permette al raggio di riflettersi e al colore dell’oggetto considerato di apparire, voglio dire, se la sua superficie più vicina —o quelle che la seguono—è uniforme. Più l’aria interessata è uniforme, più i due fenomeni presentano un colore netto. E, dal momento che l’effetto circolare appare solo su una superficie particolare o su superfici composte, di composizione particolare, non ci resta che mostrare quale aspetto devono presentare le superfici per riflettere il raggio sotto forma circolare»[3].
Dopo aver verificato che l’aria umida e densa potesse essere assimilata a una superficie riflettente, Ibn al-Haytham può quindi utilizzare le conclusioni relative alla riflessione sulle superfici sferiche concave[4] del suo Libro sull’ottica[5]. Egli cerca la condizione affinché un raggio proveniente da una fonte luminosa —un corpo celeste ad esempio, e riflesso su questa superficie, fuori dall’asse— passa attraverso l’occhio in seguito alla sua riflessione. Supponiamo, infatti, che A sia questa fonte luminosa (cfr. figura I), C il centro del cerchio prodotto dall’intersezione della sfera e con un piano qualsiasi passando per AC. Sia A’ il centro dell’occhio. Prolunghiamo ACA’ in S sulla superficie della sfera. Qual è la condizione per cui un raggio emesso da A e riflettuto in I passi per A’?
Nel suo Libro sull’ottica[6], Ibn al-Haytham dimostra che è necessario che AS/SA’ > AC/CA’. Se ora consideriamo il sistema di rivoluzione attorno ad AC, la riflessione si realizzerà allo stesso modo dai punti della circonferenza del cerchio descritto da I, di centro T e di raggio IT —la normale portata da I in T. Ibn al-Haytham pensa che un osservatore posizionato in A’ debba scorgere questi punti sotto forma di un arco di cerchio.
La condizione perché l’arcobaleno appaia è che l’occhio sia sull’asse portato dal centro della fonte luminosa al centro della sfera o porzione di sfera dell’aria densa e umida:
«È solamente quando questa posizione si verifica, scrive, che il fenomeno può apparire, ma questo non è assolutamente possibile in tutte le altre posizioni»[7].
In modo del tutto geometrico, Ibn al-Haytham cerca poi di individuare, combinando le posizioni del punto S e quelle del punto T, tutte le posizioni possibili seguendo le quali l’apparizione dell’arco cambia in grandezza. S può essere all’orizzonte, al di sopra o al di sotto, T può essere prima di A’, in A’, tra A’ e S. Se S è all’orizzonte, l’arco è un semicerchio, qualsiasi sia la posizione di T; se S si trova sotto l’orizzonte e T tra A’ e S, l’arco è più grande di un semicerchio; se T è in A’, l’arco è un semicerchio; se T si trova prima di A’, è più piccolo di un semicerchio. Questi rapporti sono inversi se S si trova sotto l’orizzonte[8].
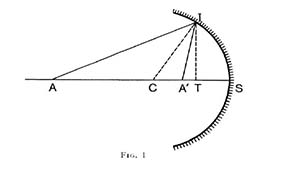
Un osservatore posizionato in A’ percepirà quindi la forma di un arco più o meno grande seguendo le posizioni di S e di T; ma vedrà anche i colori della fonte luminosa, poiché, per Ibn al-Haytham, i colori si riflettono come le luci, contemporaneamente ad esse e seguendo la stessa legge. Secondo la dottrina del Libro sull’ottica, questi colori appaiono, inoltre, mescolati a quelli del corpo riflettente. Se, d’altra parte, questo corpo non è di una trasparenza estrema, né perfettamente liscio, come l’aria densa e umida, allora:
«La visione non è assicurata e l’oggetto non appare affatto in maniera certa. È necessario che in questa nuvola il colore della fonte luminosa non appaia all’estremità, come conseguenza della colorazione della nuvola e della miscela dei due colori; poiché, non essendo estremamente trasparente, né perfettamente liscia, la visione non è assicurata. L’effetto che appare non è altro che il colore della fonte luminosa, e la sua luminosità è debole… E dal momento che il corpo luminoso ha una certa importanza, è necessario che anche la posizione della riflessione ne abbia una»[10].
Quando un osservatore ben posizionato scorge in questo caso la luce attenuata, Ibn al-Haytham sa che è a causa della riflessione, ma quando i colori ricevuti differiscono da quelli della fonte luminosa, la ragione, crede lui, sia nella natura stessa dell’aria densa e luminosa.
Da questo rapido riassunto della teoria dell’arcobaleno di Ibn al-Haytham, consideriamo per adesso due punti:
—Una supposizione che è alla base dell’intero tentativo: l’autore ammette, come la tradizione aristotelica prima di lui, la possibilità di uno studio diretto del fenomeno, cioè che tutti gli elementi che lo costituiscono sono direttamente accessibili all’esame ottico.
—Una constatazione non meno importante che concerne la natura stessa della prova: in nessun momento, nel saggio sull’arcobaleno, Ibn al-Haytham ha tentato, come ha sempre fatto, di costruire una situazione sperimentale per verificare le ipotesi geometriche. Non stupirà che uno studio diretto dell’arcobaleno non si presta per nulla, nella situazione teorica e strumentale che si conosce, a questo tipo di prova tuttavia richiesta da Ibn al-Haytham.
[1] Differenti studi rivelano anche la costanza di tale progetto; vedi ad esempio la nostra traduzione del Discorso della luce, in Revue d’Histoire des Sciences, t. XIX, no 3, luglio-settembre 1968, p. 205.
[2] [al-Fārisī], Tanqīḥ …, vol. II, p.259.
[3] [al-Fārisī],Tanqīḥ, p.263.
[4] Ibn al-Haytham pensa che la parte concava sia quella riflettente. Scrive, infatti: “I tipi di concavità nelle quali si possono immaginare i cerchi e le porzioni di cerchio variano. Ma la più regolare, quella che somiglia di più alla realtà delle parti dell’universo, la più adatta a comunicare la sua forma a questo corpo (ossia, l’aria umida) è la forma sferica, se questa è la forma dell’aria, dell’acqua e delle parti dell’universo che circondano l’aria. E, dal momento che il vapore si muove, analogamente, da una superficie sferica ad un’altra superficie sferica seguendo la stessa posizione in tutte le direzioni, è necessario che essa stessa sia sferica e che il centro della sua sfera sia quello dell’universo, che ogni sua porzione abbia questa forma o una forma simile. Ora, ciò che è più verosimile è che la concavità dell’aria umida citata sia una concavità sferica”. Vedi Tanqīḥ, p. 264.
[5] Vedi [Ibn al-Haytham], Kitāb al-Manāẓir, V parte, MS: 3215 Fatīh Istambul, pp.267 sqq. MS: 2448 Aya Sofia Istambul, pp. 465 v sqq.
[6] Vedi [Ibn al-Haytham], Kitāb al-Manāẓir, op. cit.
[7] [al-Fārisī], Tanqīḥ, p. 265.
[8] [al-Fārisī], Tanqīḥ, pp. 266-267.
[9] [al-Fārisī], Tanqīḥ, pp. 266-267.
[10] Op cit.
3. Critica di al-Fārisī alla spiegazione dell’arcobaleno di Ibn al-Haytham e passaggio al nuovo modello
Al-Fārisī, commentatore e riformatore dell’Ottica di Ibn al-Haytham nel Tanqīḥ al-Manāẓir (1309), criticando la spiegazione dell’arcobaleno di Ibn al-Haytham per restituirla alle regole della nuova ottica da egli stesso concepita, si concentra in particolar modo sulla necessità di inquadrare meglio il fenomeno da un punto di vista fisico. Infatti, al-Fārisī, riprendendo le posizioni di Avicenna, avvia il processo per giustificare una trattazione indiretta, quindi sperimentale, del fenomeno dell’arcobaleno. Accettando l’idea della teoria aristotelica che le gocce d’acqua disperse nell’atmosfera nell’istante in cui le nuvole si dissolvono in pioggia, costituiscono l’origine di un arco riprodotto per riflessione su tutte le gocce, ma rifiutando l’intervento dell’aria “densa e umida” per la formazione dello stesso, isola una sola goccia dall’insieme di tutte le gocce, compiendo il primo passo per approdare all’analogia con la sfera trasparente riempita d’acqua (Rashed, 1970, p. 121). Questo passaggio, tuttavia, sarebbe stato impossibile realizzarlo, se nella nuova ottica, Ibn al-Haytham non avesse operato una separazione netta tra la teoria della visione e quella della propagazione luminosa, conditio sine qua non per concepire la propagazione di una sola goccia separatamente dalla totalità della “pioggia leggera” (Ibid., p. 139). In un secondo momento, riprendendo i risultati di Ibn al-Haytham nel Saggio sulla sfera ardente, Al-Fārisī cerca di abbandonare la spiegazione per riflessione del fenomeno, in favore di due rifrazioni che a loro volta danno luogo, tra di esse, a una o più riflessioni (Ibid., p.121). Consapevole, tuttavia, che per una sfera riempita d’aria esistono, a causa dell’involucro di vetro, quattro rifrazioni e non solamente due, come nel caso della goccia d’acqua, per assicurare la tenuta della sua analogia, al-Fārisī ricorre a una approssimazione fornita dallo studio della rifrazione e giustificata dagli indici di trasparenza dei due corpi: infatti, poiché questi sono molto simili, il raggio può penetrare nella fiala senza rifrangersi nella maniera abitualmente considerata (Ibid., p.124). Risolto anche questo problema, al-Fārisī può quindi dare avvio alla spiegazione geometrica del fenomeno dell’arcobaleno, corroborandola finalmente con esperimenti sulla sfera trasparente riempita d’acqua.