Bacone afferma che la scienza sperimentale possiede tre grandi prerogative, la prima delle quali è quella di controllare le conclusioni delle altre scienze:
«Tale scienza sperimentale gode, rispetto alle altre scienze, di tre grandi prerogative. La prima è che essa, attraverso l’esperienza, controlla le conclusioni rilevanti di tutte le altre scienze. Infatti le altre scienze reperiscono i loro principi per mezzo di esperimenti, ma traggono le conclusioni da ragionamenti basati sui principi scoperti, perciò se si deve avere una esperienza specifica ed esauriente di tali conclusioni, occorre avvalersi dell’aiuto di questa nobile scienza» [1].
Cerchiamo ora di vedere, nel dettaglio, come il filosofo applica il suo metodo sperimentale per fare chiarezza sulla natura dell’arcobaleno e sui meccanismi che regolano questo interessante fenomeno; il brano è certamente tra i più famosi dell’Opus, e ha contribuito a creare l’immagine, alquanto fantasiosa, di Bacone quale antesignano degli scienziati del XVII secolo, attento lettore del libro della natura, in contrapposizione con gli aristotelici della sua epoca, retrogradi e dogmatici.
La disquisizione sulla natura dell’arcobaleno [2] viene riportata come esempio di applicazione del metodo sperimentale e dimostrazione di questa sua prima prerogativa. Lo studio di questo fenomeno è di pertinenza della filosofia naturale e dell’ottica, ma è necessario avvalersi anche della scienza sperimentale, per di più né Aristotele, né Avicenna, né Seneca ci hanno lasciato, al riguardo, una trattazione soddisfacente.
La prima preoccupazione dello sperimentatore sarà quella di ricercare i diversi luoghi e le diverse situazioni in cui è possibile osservare l’iride; l’elenco può essere lungo ed è basato su esperienze abbastanza comuni: l’osservatore esamina in controluce alcune particolari pietre, guarda i raggi solari illuminare le piccole gocce d’acqua sollevate dalla rotazione dei remi di una barca o delle pale di un mulino, osserva, di notte, i colori formarsi attorno alla fiamma di una candela o, al mattino, nelle gocce di rugiada, e compie molte altri esperimenti simili. Già queste prime osservazioni portano ad alcune scoperte: ad esempio che la formazione dei colori nella lapis Hiberica non dipende, come ritengono alcuni, dalla forma esagonale della pietra, perché il fenomeno si è osservato anche in pietre di forma diversa, né dal colore bianco della sua superficie, perché l’iride si può vedere anche attraverso i cristalli scuri. Il semplice elenco di alcune esperienze quindi permette di confutare talune credenze infondate. Lo sperimentatore però non si limiterà ad accumulare osservazioni, ma cercherà di individuare delle costanti nella diversità di manifestazioni del fenomeno: la prima è che la disposizione dei colori in tutte queste situazioni, dai cristalli alle gocce di rugiada, è analoga a quella che si forma nell’arcobaleno.
Per proseguire l’indagine sperimentale occorre poi munirsi dell’astrolabio, che permette di determinare l’altezza dell’arcobaleno sull’orizzonte; con l’uso di questo strumento possiamo stabilire che:
a) l’arcobaleno è sempre situato dalla parte opposta al sole, e una sola linea congiunge il centro del sole, il centro dell’occhio dell’osservatore e il centro dell’arcobaleno;
b) tanto più il sole è alto, tanto più in basso si trova l’arcobaleno, la linea immaginaria di cui sopra è come un’asta il cui perno ruota intorno all’occhio dell’osservatore: quando una estremità si innalza l’altra si abbassa;
c) quando il sole è all’orizzonte, ossia all’alba o al tramonto, l’arcobaleno può raggiungere la sua altezza massima, che è di 42 gradi, viceversa, quando il sole supera l’altezza di 42 gradi l’arcobaleno non è più visibile.
Siamo di fronte ad un raro esempio di uso, nel medioevo, della misurazione in questioni di filosofia naturale, il valore dell’altezza massima dell’arcobaleno non si trova in nessun altro autore precedente, [3] ed è forse l’unico caso in cui possiamo essere certi che Bacone ha effettivamente compiuto gli esperimenti di cui tratta, e non li ha semplicemente letti in qualche testo arabo o greco. L’autore si dimostra tra l’altro molto preciso su questo punto, e si dilunga in questioni generali intorno alla misurazione dell’altezza degli astri, precisando, tra l’altro, che, nel caso dell’arcobaleno e degli altri oggetti che si trovano nell’aria al di sotto del cielo della luna (le comete, ad esempio, erano considerate tali), si deve tener conto anche della statura dell’osservatore, perché essa non è trascurabile, al contrario di quanto avviene per i corpi lontani, il sole e le stelle.
L’aver rilevato empiricamente un’altezza massima del sole, al di sopra della quale l’arcobaleno non è più osservabile, ci fornisce una semplice regola generale per prevedere i tempi e i luoghi nei quali il fenomeno è visibile: sappiamo così, ad esempio, anche senza verificarlo direttamente, che al tropico del Cancro non è possibile vedere l’arcobaleno a mezzogiorno in nessun periodo dell’anno, perché l’astronomia ci dice che in quei luoghi, anche nel solstizio d’inverno, l’altezza del sole di mezzogiorno è maggiore di 42 gradi. Bacone si cura di precisare anche il modo in cui si deve calcolare l’altezza del sole a mezzogiorno alle varie latitudini e nei vari giorni dell’anno, cioè con un computo che oggi sintetizzeremmo nella formula α=90°- β - γ (essendo α l’altezza del sole di mezzogiorno, β la latitudine del luogo e γ la declinazione del sole).
Siamo finalmente in grado di avere una rappresentazione geometrica, ossia un modello, che renda ragione della varietà di manifestazioni del fenomeno. Noi infatti osserviamo l’arcobaleno presentarsi in forme diverse: talvolta, presso cascate o irrigazioni, si può vedere l’iride formare un cerchio completo, nelle nubi invece è visibile solo un semicerchio, o una porzione più piccola di cerchio, l’arco è ora più alto ora più basso. La diversa forma e grandezza che l’arcobaleno acquista, a seconda dei luoghi e delle circostanze, si spiega con un modello geometrico che l’osservatore attento può facilmente scoprire: si immagini dunque un cono il cui vertice è nell’occhio dell’osservatore, il cui asse è la linea che passa attraverso il centro del sole, il centro dell’occhio e il centro dell’arcobaleno fino al nadir del sole, il cerchio dell’iride sarà la base di questo cono, e si innalzerà e abbasserà in rapporto all’innalzamento o abbassamento del sole.
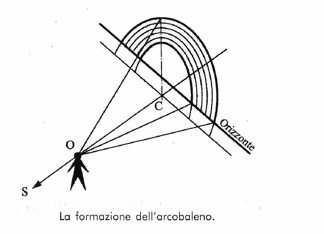
La distanza tra l’occhio dell’osservatore e la barriera di gocce d’acqua determina l’altezza del cono; minore è l’altezza, maggiore è la porzione di circonferenza che riusciamo a vedere, questo spiega il motivo per cui presso le cascate possiamo a volte vedere il cerchio completo: l’altezza del cono, in questo caso relativamente piccola, fa sì che la base rimanga interamente al di sopra dell’orizzonte. Quando invece vediamo l’arcobaleno sulle nubi la base del cono, a causa della maggiore distanza, è troppo grande e viene in parte tagliata dall’orizzonte.
Sin qui l’osservazione ha permesso di comprendere la struttura geometrica dell’arcobaleno senza dirci nulla della natura dei raggi che lo formano: si tratta di raggi riflessi o rifratti? I colori dell’iride sono reali o si tratta di un inganno della vista? per rispondere a queste domande occorre compiere altre esperienze, peraltro piuttosto semplici. L’osservatore che si muove, a piedi o a cavallo, parallelamente all’arcobaleno, vede l’arco muoversi insieme a lui con la medesima velocità e nella stessa direzione; similmente, se si mette a correre verso l’arcobaleno lo vedrà indietreggiare, oppure avanzare se invece si allontana. Un analogo movimento apparente si nota nel sole ed è dovuto alla grande distanza che c’è tra noi e l’astro, per lo stesso motivo i raggi solari ci appaiono tutti paralleli tra loro:
«Se mille uomini si disponessero lungo un’unica fila da oriente ad occidente, la vista giudicherebbe le loro ombre parallele [...] a causa dell’eccessiva distanza [dal sole]» [4].
Questo movimento apparente, identico nel sole e nell’arcobaleno, unito al fatto che quest’ultimo si vede sempre in opposizione al sole, ci porta a concludere che l’iride non sia altro che l’immagine del sole riflessa su una nube: i raggi che la formano sono dunque riflessi.
I raggi rifratti infatti hanno un comportamento diverso: sono, ad esempio, quelli che fanno apparire scura una nube molto densa e bianca una nube più rarefatta, ma in tal caso diversi osservatori vedono da differenti posizioni lo stesso colore nello stesso luogo, cosa che non avviene nel caso dell’iride, in cui ogni osservatore vede il “suo” arcobaleno:
«C’è un arcobaleno per ogni persona che lo guarda [...]: è impossibile che due persone vedano lo stesso e identico arcobaleno, anche se la persona inesperta non se ne accorge. [...] Tanti sono gli osservatori, quanti sono gli arcobaleni» [5].
Diverso è anche il caso dell’iride che si forma nei cristalli: qui il colore è formato da raggi rifratti, per questo non segue l’osservatore nei suoi spostamenti.
A questo punto è utile richiamare alcuni concetti che Bacone tratta nella sezione dedicata all’ottica, in merito alle immagini riflesse. Nella figura è rappresentato il caso dello specchio piano: l’immagine posta in A si riflette nel punto B ma per l’osservatore O essa appare nel punto D; l’immagine dell’oggetto appare quindi nel punto in cui il raggio visuale OD incontra la linea AD che unisce l’oggetto alla sua immagine. Partendo dall’ipotesi che l’angolo di incidenza è uguale a quello di riflessione, Bacone dimostra che BA è uguale a BD. [6]
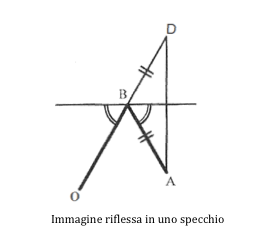
Qualcosa di simile avviene negli specchi sferici, però in tal caso «l’oggetto appare nel punto d’incontro tra il raggio visuale e la linea dall’oggetto al centro della sfera» [7].
È importante rilevare che, sia nel caso dello specchio sferico che di quello piano si osserva un cambiamento del punto di riflessione in concomitanza con lo spostamento dell’osservatore: allora, giacché osserviamo l’arcobaleno muoversi seguendo i nostri spostamenti, occorre ammettere che anche il punto di riflessione si muove, ossia che l’immagine viene riflessa da un insieme di goccioline (o piccoli specchi sferici) differente per ogni singola posizione. Si deve poi pensare che lo spostamento del punto di riflessione non avviene solo sulla superficie della nube ma anche in profondità, diversamente infatti non si spiegherebbe la mobilità dell’arcobaleno in relazione agli spostamenti dell’osservatore. Quando l’osservatore si muove verso l’arcobaleno questo viene visto indietreggiare, infatti con lo spostamento dell’occhio si sposta anche la base del cono di cui si è detto sopra, la riflessione avverrà quindi su di un insieme di goccioline posto più indietro.
Perché questo avvenga si deve ammettere che l’arcobaleno sia visibile solo in determinate condizioni di oscurità della nube: quando l’osservatore si avvicina i vapori che prima riflettevano l’immagine sono ora troppo illuminati, quindi si potranno percepire solo quei raggi che sono riflessi dalle gocce poste più in profondità nella nube:
«Quando l’occhio si muove in direzione dell’arcobaleno, subito lo sguardo raggiunge un tratto di aria più lontano che è rischiarato, e si avvicina ad un luogo più prossimo all’arcobaleno, così che, a causa dell’avvicinamento dell’osservatore, lo stesso luogo non si trova più nelle medesime condizioni, è anzi più illuminato di quanto sia necessario affinché l’arcobaleno sia visibile. [...] Per questo bisogna che la base del cono ricada in un punto più profondo della nube, ove ci sia sufficiente oscurità» [8].
Qualcosa di analogo si può osservare nella nebbia: da lontano la vista può essere bloccata dalla densità dei vapori, da vicino invece lo sguardo è in grado di penetrarli.
Veniamo ora alla seconda questione, cioè la natura dei colori dell’iride. Il fatto, comprovato dall’esperienza, che esistano tanti arcobaleni quanti sono gli osservatori induce a ritenere che i colori che si vedono non siano reali:
«Nell’arcobaleno non vi sarà che la parvenza dei colori, e solo quando l’arcobaleno è visibile. Si è detto infatti che l’arcobaleno cambia a seconda dell’osservatore. Ma non è l’osservazione che produce i colori, è chiaro infatti che lo sguardo non può creare i colori nella nube, per cui vi sarà soltanto la parvenza [dei colori]» [9].
Bacone considera “reali” i colori generati dalle particolari qualità della superficie dell’oggetto che appare colorato: è il caso, ad esempio, dell’iride che si osserva in certi cristalli. I colori reali esistono anche se non c’è nessuno a guardarli. Diverso è invece quello che avviene nell’arcobaleno, in cui il colore esiste solo in quanto c’è qualcuno che lo guarda, ed è quindi causato da un difetto della vista, come avviene in altri casi analoghi: si possono vedere infatti i colori dell’iride osservando, con gli occhi socchiusi, le gocce di rugiada o un raggio solare che penetra in una stanza buia attraverso un foro, questo accade soprattutto alle persone miopi. Quindi è solo la debolezza della vista a produrre i colori. Questa conclusione è collegata alla teoria baconiana che assegna all’occhio un ruolo attivo nel meccanismo della visione. Bacone cerca una soluzione che concili le due posizioni opposte, di coloro che sostenevano che la visione avvenisse per l’immissione nell’occhio dei raggi provenienti dall’oggetto vista, e coloro che ritenevano fosse l’occhio ad emettere dei raggi visivi: secondo Bacone la visione nasce dall’incontro tra i raggi luminosi provenienti dall’oggetto e i raggi visivi provenienti dall’occhio; quando l’asse immaginario condotto dal nervo ottico attraverso i due occhi si sovrappone all’asse congiungente l’oggetto e l’occhio si ha la visione ottimale, in tutti gli altri casi la visione è imperfetta e si possono generale inganni, come appunto avviene per colori dell’arcobaleno. L’idea che nell’arcobaleno non vi siano colori reali ma soltanto parvenze di colori (apparentia colorum) si trova già in autori antichi come Artemidoro e Posidonio, e veniva contestata da Alberto Magno nel suo commento alla Meteorologia di Aristotele:
«Appare assurdo che essi [Artemidoro e Posidonio] affermino che nell’arcobaleno non vi sono veri colori. Dal momento che la luce di ogni colore è una ipostasi e una forma sostanziale e produce i colori dipinti attraverso i suoi raggi che attraversano un mezzo denso trasparente, ne consegue che vi sono veri colori. [...] Quindi l’opinione dei Pitagorici è infondata. [...] L’errore è dovuto alla mancata distinzione tra I) la causa materiale del colore, II) la causa formale del colore. La causa materiale dell’arcobaleno risiede nelle qualità del soggetto in cui si trova [...], la causa formale del colore è dovuta alla luce» [10].
Come si può vedere Alberto Magno formula la questione in termini strettamente aristotelici: il colore, che si trova in potenza nel soggetto materiale, viene posto in atto dalla luce, che ne è la causa formale, dunque è reale, in quanto costituito dall’unione di forma e materia. Come nota Hackett: «Ciò che separa Bacone da Alberto è la sua adesione all’analisi stoica del problema dell’arcobaleno come distinta da una risposta aristotelica» [11].
L’ultima questione è, a giudizio di Bacone, la più delicata e riguarda la forma dell’arco: su questo punto sono state formulate, dagli altri autori, due diverse ipotesi, entrambe respinte da Bacone. La prima vuole che l’arcobaleno si formi in una massa di vapori di forma conica e abbia pertanto la forma della base di tale cono: questa idea è da escludere, perché sappiamo per esperienza che l’arco si forma in nuvole di vapori dalle forme più svariate. La seconda ipotesi menzionata prevede che l’arcobaleno sia generato da una triplice rifrazione di raggi solari, e formi un cono, la cui base assuma una forma non perfettamente circolare, forse ellittica, per quanto si riesce a dedurre dal testo [12]. Era questa l’opinione di Grossatesta, che però Bacone non nomina esplicitamente, pur citando testualmente dal suo trattato.
Bacone invece sostiene la perfetta circolarità dell’arco, e lo dimostra col seguente ragionamento: poiché la diversità dei colori dipende dalla diversa posizione dell’oggetto riflettente rispetto al raggio di luce, ne consegue che i punti nei quali osserviamo uno stesso colore debbano avere la medesima posizione rispetto al raggio solare e all’occhio dell’osservatore, ora, poiché nell’arcobaleno un determinato colore si dispone lungo una linea curva da un’estremità all’altra, tale curva non può che essere una circonferenza, i cui punti mantengono tutti la medesima distanza dal centro. È interessante notare che Bacone, nella teoria dell’arcobaleno, si distacca in modo rilevante dal suo maestro Roberto Grossatesta il quale, su questa tema, aveva composto un’opera dal titolo De iride et speculo. Grossatesta riteneva infatti che il fenomeno fosse dovuto ai raggi rifratti, mentre Bacone, come abbiamo visto, lo imputava ai raggi riflessi. La critica alle opinioni di Grossatesta è molto precisa e puntuale e non mancano, nel testo di Bacone, citazioni testuali tratte dall’opera del vescovo di Lincoln che però, come si è già detto, non viene mai nominato.
A questo punto può essere interessante conoscere quale posto occupa la teoria baconiana dell’arcobaleno nella storia della scienza, quanto la sua spiegazione si discosta da quella attualmente accettata e quali possono essere stati i suoi contributi alla comprensione di questo fenomeno meteorologico piuttosto complesso. Oggi sappiamo che l’arcobaleno si forma in seguito alla riflessione e rifrazione della luce solare, quando questa attraversa uno strato d’atmosfera ricco di goccioline d’acqua dal diametro molto piccolo. Nel cosiddetto arcobaleno primario, la cui gamma di colori va dal violetto all’interno fino al rosso verso l’esterno, il raggio luminoso subisce una prima rifrazione verso l’interno della gocciolina, quindi una riflessione, in cui la sequenza dei colori nello spettro viene invertita, infine una seconda rifrazione all’uscita dalla massa acquosa. Nel caso dell’arcobaleno secondario, invece si ha una doppia riflessione del raggio all’interno della goccia, col risultato che la serie dei colori va dal rosso all’interno fino al violetto verso l’esterno, risultando cosi invertita rispetto all’arcobaleno primario.
Questa spiegazione si trova per la prima volta nel De iride et radialibus impressionibus, composto da Teodorico di Vriberg nei primi anni del XIV secolo, e costituisce un altro interessante esempio di utilizzo del metodo sperimentale nel medioevo [13]. Solo nel 1637 Cartesio darà alla teoria di Teodorico una formulazione matematica rigorosa, sulla base della “legge dei seni” da lui scoperta: egli determinò l’angolo di incidenza che devono avere i raggi solari sulle gocce, per essere percepiti dall’osservatore, dando così una spiegazione analitica del valore, ottenuto empiricamente da Bacone, dell’altezza massima del sole, oltre la quale l’arcobaleno non è più visibile [14]. Nel 1837 G.B. Airy ampliò la teoria di Cartesio, sulla base delle nuove conoscenze intorno alla diffrazione luminosa, scoprendo una relazione tra l’intensità dei colori e la dimensione delle gocce d’acqua.
Dunque la disquisizione di Bacone apporta oppure no un contributo al progresso della conoscenza? Nonostante l’opinione contraria di altri studiosi [15], Lindberg [16] sostiene che la teoria di Bacone segna un progresso nella via della corretta spiegazione del fenomeno, in due punti in particolare: 1) nel sottolineare il ruolo essenziale della riflessione, confutando la teoria grossatestiana che considerava la sola rifrazione dei raggi 2) nell’affermare che l’arcobaleno non si forma nell’intera nuvola ma in un gruppo di gocce d’acqua che cambia a seconda della posizione dell’osservatore.
Note
[1] R. Bacone, Opus Maius, II, p. 172 (edited by J.H. Bridges, Oxford 1879-1890): «Et haec scientia experimentalis habet tres magnas praerogativas respectu aliarum scientiarum. Una est quod omnium illarum conclusiones nobiles investigat per experientiam. Scientiae enim aliae sciunt sua principia invenire per experimenta, sed conclusiones per argumenta facta ex principiis inventis. Si vero debeant habere experentiam conclusionum suarum particularem et completam, tunc oportet quod habeant per adjutorium istius scientiae nobilis».
[2] Opus Maius, II, pp. 172-201.
[3] D. Lindberg, “Light, vision, and the universal emanation of forces”, in J. Hackett ed.), Roger Bacon and the sciences, Brill, Leiden - New York 1997, p. 270.
[4] Opus Maius, II, p. 187: «Si mille homines ordinentur secundum lineam unam ab oriente ad occidens, umbrae eorum essent aequidistantes secundum sensum [...] propter nimiam distantiam».
[5] Ibidem: «Iris numeratum secundum numerum hominum aspicientium [...] impossibile est quod duo videant unam et eandem iridem, quamvis inexpertus hoc non percipiat [...] quot sunt videntes, tot sunt irides».
[6] Ibidem, II, p. 135.
[7] Ibidem, II, p. 136: «Secundum iudicium visus apparet res in cuncursu radii visualis cum linea ducta a re in centrum sphaerae».
[8] Ibidem, p. 189: «Quando oculus mutatur in partem iridis, iam attingit aerem ulteriorem qui lucidus est et appropinquat ad locum priorem iridis, ita quod propter approximationem videntis, iam non invenitur locus idem eiusdem dispositionis, immo clarior quam requiratur ad iridis apparitionem [...] ideo oportet quod basis pyramidis cadat in nube ulterius in loco debitae obscuritatis».
[9] Ibidem, II, p. 190: «Nihil erit in loco iridis nisi apparentia colorum, et non erit nisi quando apparet. Nam dictum est quod secundum diversitatem aspicientium diversificatur iridis. Sed aspectus non facit colores. Visus enim non potest creare colores in nube, ut patet; quare nihil erit nisi per apparentiam».
[10] Albertus Magnus, Tractatus IV, Meteorologica III, ed. Borgnet, Ch. XI , p. 679.
[11] J. Hackett, “Roger Bacon on scientia experimentalis”, in Roger Bacon and the Sciences, commemorative essays, p. 303.
[12] Opus Maius, II, p. 194: «Se diffundunt non in pyramidem rotundam [...] sed in assimilatam curvae superficiei pyramidis rotundae».
[13] A.C. Crombie, Da Sant’Agostino a Galileo. Storia della scienza dal V al XVII secolo, Feltrinelli, Milano 1970, pp. 93-96.
[14] W.R. Shea, La Magia dei Numeri e del Moto, Boringhieri, Torino 1994, pp. 205ss.
[15] C.B. Boyer, The rainbow. From myth to Mathematics, T. Yoseloff, New York - London 1959, pp. 92-102.
[16] D. Lindberg, “Roger Bacon’s Theory of the Rainbow: Progress or Regress?”, in Isis, 57 (1966), pp. 235-248.
L. Tampellini, Ruggero Bacone. Un passaggio nodale all'origine della scienza moderna, Cantagalli, Siena 2004, pp. 115-128