La bellezza e la ricerca della bellezza nella scienza

L'argomento che mi è stato chiesto di trattare è difficile, se si devono evitare banalità e luoghi comuni. Inoltre le mie conoscenze e la mia esperienza, quali che siano, mi costringono a limitarmi per intero agli aspetti teorici delle scienze fisiche: una limitazione molto grave. Devo cominciare perciò col chiedere la vostra pazienza e indulgenza.

Noi tutti siamo sensibili alla bellezza della natura. Non è irragionevole che qualche aspetto di questa bellezza sia condiviso dalle scienze della natura. Ci si può chiedere però in quale misura la ricerca della bellezza sia un obiettivo dell'attività scientifica. In proposito si è espresso con grande chiarezza Poincaré, che ha scritto in un suo saggio:

«Lo scienziato non studia la natura perché sia utile farlo. La studia perché ne ricava piacere; e ne ricava piacere perché è bella. Se la natura non fosse bella, non varrebbe la pena di sapere e la vita non sarebbe degna di essere vissuta {...}. Intendo riferirmi a quell'intima bellezza che deriva dall'ordine armonioso delle parti e che può essere colta da un'intelligenza pura».

E continua:

«Proprio perché la semplicità e la vastità sono entrambe belle noi cerchiamo di preferenza fatti semplici e fatti vasti; e traiamo piacere ora dal seguire il corso immenso delle stelle ora dall'osservare con un microscopio quella prodigiosa piccolezza che è anche una vastità, e ora nel ricercare nelle ere geologiche quei segni del passato che ci attraggono per loro lontananza».

Commentando queste osservazioni di Poincaré, J.W.N. Sullivan, l'autore di acute biografie di Newton e di Beethoven, scrisse (in «Athenaeum», maggio 1919):

«Poiché l'oggetto primario della teoria scientifica è quello di esprimere le armonie che si osservano in natura, vediamo subito che queste teorie devono avere un valore estetico. La misura del successo di una teoria scientifica è, in effetti, una misura del suo valore estetico, essendo una misura dell'estensione in cui ha introdotto armonia in quello che in precedenza era caos. È nel suo valore estetico che si trova la giustificazione della teoria scientifica, e con essa la giustificazione del metodo scientifico. Poiché fatti senza leggi non presenterebbero alcun interesse, e leggi senza teorie avrebbero, al massimo, solo un'utilità pratica, vediamo che i motivi che guidano lo scienziato sono, fin dal principio, manifestazioni dell'impulso estetico {...}. La misura in cui la scienza è inferiore all'arte è la misura in cui è incompleta come scienza».

Nel saggio Art and Science, l'eminente critico d'arte Roger Fry (nato anche per la sua biografia di Virginia Woolf) comincia citando Sullivan e continua:

Sullivan dice audacemente: «È nel suo valore estetico che si trova la giustificazione della teoria scientifica, e con essa la giustificazione del metodo scientifico». Vorrei porre a questo punto a S. {Sullivan} la domanda se una teoria che trascurasse i fatti avrebbe per la scienza lo stesso valore di una teoria in accordo con i fatti. Suppongo che direbbe di no; eppure non riesco a vedere alcuna ragione estetica per cui non dovrebbe avere lo stesso valore.

Tornerò sulla domanda posta da Roger Fry e suggerirò una risposta diversa da quella che Fry presume avrebbe data Sullivan. Ora passerò però a considerare le osservazioni in cui Fry mette a confronto gli impulsi di un artista e di uno scienziato.

«Dai più elementari rudimenti della sensazione pura sino ai massimi sforzi di disegno intenzionale, ogni punto in questo processo artistico è inevitabilmente accompagnato da piacere e questo processo è impossibile senza di esso {...}. È vero anche che il riconoscimento dell'inevitabilità nel pensiero è accompagnato normalmente da un'emozione piacevole; e che il desiderio di questo piacere mentale è la forza motrice che spinge alla formazione della teoria scientifica. Nella scienza l'inevitabilità dei rapporti rimane egualmente definita e dimostrabile, sia che l'emozione si accompagni o no ad essa, mentre in arte un'armonia estetica semplicemente non esiste senza lo stato emozionale. L'armonia in arte non è vera se non è sentita come emozione {...}. In arte il riconoscimento di rapporti è immediato e a livello della sensazione: forse dovremmo considerarlo curiosamente affine a quei casi di geni matematici che hanno un'intuizione immediata di rapporti matematici che non sono in grado di dimostrare».

Vorrei ora passare da queste generalità a esempi particolari di ciò che gli scienziati hanno considerato bello. Il mio primo esempio è connesso all'osservazione di Fry concernente ciò che i geni matematici percepiscono come vero senza alcuna causa apparente. Il matematico indiano Srinivasa Ramanujan (di cui alcuni di voi conosceranno il modo clamoroso in cui pervenne alla fama matematica nel 1915) lasciò un gran numero di taccuini (uno dei quali fu scoperto solo qualche anno fa). Nei taccuini Ramanujan registrò varie centinaia di formule e di identità. Molte di queste sono state dimostrate solo recentemente con metodi che Ramanujan non poteva conoscere. G.N. Watson, che ha speso vari anni della sua vita a dimostrare molte delle identità di Ramanujan, ha scritto:

«Lo studio dell'opera di Ramanujan e il problema a cui essa da origine richiama inevitabilmente alla mente l'osservazione di Lame che quando si leggono gli articoli di Hermite sulle funzioni modulari «On a la chair de poule (viene la pelle d'oca)». Io vorrei esprimere il mio atteggiamento con maggiore prolissità dicendo che una formula come

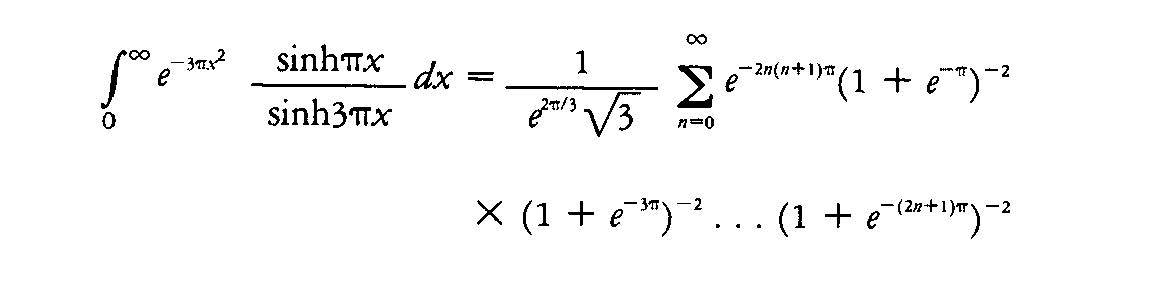
mi dà un'emozione che è indistinguibile da quella che provo quando erro nella Sagrestia Nuova di San Lorenzo, a Firenze, e vedo dinnanzi a me l'austera bellezza del Giorno, della Notte, del Crepuscolo e dell'Aurora, che Michelangelo ha posto sulle tombe di Giuliano e di Lorenzo de' Medici».

Un esempio di tipo molto diverso è fornito dalla reazione di Boltzmann a uno dei saggi di Maxwell sulla teoria dinamica dei gas, in cui Maxwell mostra come si possa trovare una soluzione esatta per i coefficienti di trasporto in un gas in cui la forza intermolecolare varia come l'inverso della quinta potenza della distanza intermolecolare. Ecco le parole di Boltzmann:

«Come un musicista può riconoscere il suo Mozart, Beethoven o Schubert dopo avere ascoltato le prime battute, può riconoscere il suo Cauchy, Gauss, Jacobi, Helmholtz o Kirchhoff dopo le primissime pagine. Gli autori francesi si rivelano con la loro estrema eleganza formale, mentre gli inglesi, specialmente Maxwell, si distinguono per il loro senso teatrale. Chi, per esempio, non ha familiarità con le memorie di Maxwell sulla sua teoria dinamica dei gas? {...} Le variazioni delle velocità sono sviluppate dapprima maestosamente; poi da un lato entrano le equazioni di stato; e dall'altro le equazioni del moto in un campo centrale. Ancora più in alto sale il caos delle formule. D'improvviso udiamo, come da timpano, le quattro battute «poni n = 5». II cattivo spirito V (la velocità relativa delle due molecole) svanisce e, come in musica, una figura finora dominante nel basso viene improvvisamente ridotta al silenzio, ciò che era parso insuperabile è stato eliminato come per un colpo di bacchetta magica {...}. Non è questo il momento di chiedersi il perché di questa o quella sostituzione. Se non si è trasportati da questi sviluppi, è meglio mettere da parte il saggio di Maxwell. Egli non scrive musica a programma con note esplicative {...}. Un risultato si sussegue a un altro in rapida successione finché, come in un'acme inattesa, perveniamo alle condizioni per l'equilibrio termico assieme alle espressioni per i coefficienti di trasporto. Allora cala il sipario!»

Ho cominciato con questi due esempi semplici per sottolineare che non occorre cercare alle scale massime per trovare la bellezza nella scienza. Sono però le scale maggiori a fornire gli esempi più significativi. Mi limiterò qui a considerarne una.

La scoperta della teoria della relatività generale da parte di Einstein è stata descritta da Hermann Weyl come un esempio supremo del potere del pensiero speculativo, mentre Landau e LifSitz la considerano come probabilmente la più bella fra tutte le teorie fisiche esistenti. E lo stesso Einstein scrisse al termine del primo articolo in cui annunciava le sue equazioni di campo: «Difficilmente chiunque comprenda a fondo questa teoria può sottrarsi alla sua magia». Passerò in seguito a considerare dove risieda la fonte di questa magia.

Vorrei tornare invece alla domanda di Roger Fry citata in precedenza, ossia come si dovrebbe considerare una teoria esteticamente soddisfacente ma ritenuta non vera.

Una volta Weyl disse a Freeman Dyson, a quanto ricorda quest'ultimo: «Nelle mie ricerche mi sforzai sempre di unire il vero al bello; ma quando dovetti scegliere fra l'uno e l'altro, di solito scelsi il bello». Io chiesi a Dyson se Weyl gli avesse fatto un esempio in proposito. Appresi cosi che l'esempio fatto da Weyl era stato quello della sua teoria di gauge della gravitazione, da lui sviluppata nel libra Raum Zeit-Materie (Spazio, tempo, materia) {1918}. A quanto pare Weyl era convinto che la sua non fosse una vera teoria della gravitazione; essa era nondimeno così bella che egli non voleva abbandonarla e quindi la conservò per la sua bellezza. In seguito l'istinto di Weyl si rivelò giusto, quando il formalismo dell'invarianza di gauge fu incorporato nell'elettrodinamica quantistica.

Un altro esempio, non menzionato da Weyl ma su cui Dyson richiamò l'attenzione, è l'equazione d'onda relativistica a due componenti del neutrino. Per una trentina d'anni i fisici ignorarono quest'equazione di Weyl perché violava l'invarianza della parità. Ancora una volta risultò che l'istinto di Weyl era giusto.

Abbiamo quindi delle prove che una teoria sviluppata da uno scienziato dotato di una sensibilità estetica eccezionalmente ben sviluppata può risultare vera anche se non sembrava tale al tempo della sua formulazione. Come scrisse molto tempo fa Keats, «ciò che l'immaginazione coglie come bellezza dev'essere verità, sia essa esistita o no in precedenza».

È in effetti incredibile che ciò che la mente umana, nei suoi stati più profondi, percepisce come bello trovi la sua realizzazione nella natura esterna. Quel che è intellegibile è anche bello.

Possiamo chiederci: come accade che la bellezza nelle scienze esatte diventi riconoscibile ancor prima che venga intesa nei particolari e prima di poter essere dimostrata razionalmente? In che cosa consiste questo potere di illuminazione?

Queste domande hanno incuriosito molti pensatori fin dai tempi più antichi. Così Heisenberg ha richiamato l'attenzione, proprio in questo contesto, sul seguente pensiero espresso nel Fedro platonico:

«L'anima è intimorita e rabbrividisce alla vista del bello, sentendo che in se stessa viene suscitato qualcosa che non le fu impartito dall'esterno attraverso i sensi, ma che è sempre stato presente in lei nella ragione profondamente inconscia».

Lo stesso pensiero è espresso nel seguente aforisma di David Hume: «La bellezza delle cose esiste nella mente che le contempla». Keplero fu così colpito dall'armonia della natura quale gli fu rivelata dalla scoperta delle leggi dei moti planetari da scrivere nella Harmonice mundi:

«Ora, ci si potrebbe chiedere in che modo questa facoltà che non ha parte nel pensiero concettuale e non può avere perciò alcuna conoscenza anteriore di rapporti armonici, possa essere capace di riconoscere ciò che è dato nel mondo esterno {...}. Rispondo a questo che tutte le idee pure, o modelli archetipi di armonia, come quelli di cui stiamo parlando, sono intrinsecamente presenti in coloro che sono capaci di apprenderle, ma non sono ricevute dapprima nella mente in virtù di un processo concettuale, essendo piuttosto il prodotto di una sorta di intuizione istintiva ed essendo innate in quegli individui».

Più recentemente Wolfgang Pauli, sviluppando queste idee di Keplero, ha scritto:

«Il ponte che conduce dai dati inizialmente disordinati dell'esperienza alle idee consiste in certe immagini primeve esistenti nell'anima: gli archetipi di Keplero. Queste immagini primeve non dovrebbero essere localizzate nella coscienza o messe in relazione a idee specifiche razionalmente formulabili. Si tratta, piuttosto, di forme apparenti alla regione inconscia dell'anima umana, immagini di possente contenuto emozionale, che non sono pensate, ma contemplate, per così dire, come figure. Il piacere che si prova nel diventare consapevoli di un nuovo elemento di conoscenza deriva dal modo in cui tali immagini preesistenti vengono a essere congruenti col comportamento degli oggetti esterni».

Pauli conclude: «Non si dovrebbe mai dichiarare che le tesi espresse mediante una formulazione razionale siano gli unici presupposti possibili della ragione umana».

Questa congruenza fra immagini preesistenti e realtà esterna a cui si riferisce Pauli, una volta sperimentata intensamente, sembra avere la conseguenza di sviluppare nella persona che ha avuto tale esperienza una fiducia eccessiva nel proprio giudizio e nei propri valori. Come si potrebbero spiegare altrimenti affermazioni come quelle, fatte da alcuni grandi scienziati, citate qui di seguito?

«La termodinamica è impazzita», affermazione fatta da Lord Kelvin, uno fra i fondatori della termodinamica, commentando la derivazione della legge ed Wien e Stefan a opera di Boltzmann.

«Lei considera la cosa dal punto di vista della stella, io la considero dal punto di vista della Natura», affermazione di Eddington in una discussione con me.

«Io sono in disaccordo con la maggior parte dei fisici di oggi proprio su questo punto», affermazione di Dirac nel contesto delle sue opinioni sui metodi di rinormalizzazione nell'elettrodinamica quantistica.

«Sembrava davvero che, per la prima volta, avessimo una cornice di riferimento abbastanza vasta da poter includere in essa l'intero spettro delle particelle elementari e delle loro interazioni, realizzando così il mio sogno del 1933», affermazione fatta da Heisenberg nel 1957 nel contesto della sua sfortunata collaborazione con Pauli su una teoria del campo unificato.

«Dio non gioca a dadi», affermazione di Einstein; o, ancor più provocatoriamente: «Quando giudico una teoria fisica, mi chiedo se, nei panni di Dio, avrei fatto l'universo in quel modo», altra affermazione di Einstein.

Nel contesto di queste ultime affermazioni di Einstein, può esser bene ricordare la rimostranza di Bohr: «Non è affar nostro prescrivere a Dio come dovrebbe governare il mondo!»

È forse in relazione a questa certezza eccessiva che dovremmo tentare di capire la relativa sterilità di menti un tempo grandi. Come infatti ha scritto Claude Bernard: «Coloro che hanno una fede eccessiva nelle loro idee, non sono adatti a fare scoperte». È chiaro che mi sto muovendo su un terreno pericoloso. Esso mi fornisce però l'opportunità di richiamare l'attenzione su un fatto che è stato occasione per me di un grande imbarazzo: esso riguarda i modi molto diversi - così almeno mi sembrano - in cui grandi scrittori, poeti e musicisti, da un lato, e grandi scienziati dall'altro sembrano crescere e maturare.

Non è insolito che, nel considerare le opere di un grande scrittore o di un grande musicista, si distinguano un periodo iniziale, un periodo di mezzo e un periodo tardo. E quasi sempre si dà il caso che la progressione dal periodo iniziale a quello di mezzo, a quello tardo sia caratterizzata da una crescente profondità ed eccellenza. In alcuni casi, come quelli di Shakespeare e di Beethoven, le ultime opere sono quelle più grandi. Questo fatto è descritto con grande efficacia da J. Dover Wilson nella sua descrizione della crescita dell'arte di Shakespeare nelle sue grandi tragedie:

«Dal 1601 al 1608 egli è assorbito nella tragedia; e la via che egli calca in questi anni può essere paragonata a un sentiero di montagna che, salendo dapprima dolcemente dalla pianura, diventa sempre più stretto finche, al culmine dell'ascesa, si fa sottile come la lama di un rasoio, una cresta glaciale con abissi da entrambi i lati, tornando a offrire una superficie più sicura al piede quando di nuovo si allarga per scendere gradualmente nella valle al di là. Shakespeare compose otto tragedie. La prima, Giulio Cesare, scritta un po' prima del periodo tragico vero e proprio, è una tragedia di debolezza, non di malvagità. In Amleto le forze del male sono attive e rovinose, benché la nota prevalente sia ancora la debolezza di carattere. Otello ci dà la prima creazione da parte di Shakespeare di un personaggio totalmente malvagio, e al tempo stesso la vittima di Iago è senza colpa: alla debolezza umana non è più consentito di dividere la responsabilità col cielo. Re Lear ci trasporta sul margine dell'abisso, poiché qui si accumulano orrore su orrore e pietà su pietà per comporre il più grande monumento all'infelicità e alla disperazione umana nella letteratura mondiale {...}. In Re Lear Shakespeare giunse molto vicino alla follia».

Eppure tirò avanti: Macbeth, Antonio e Cleopatra, (una delle sue tragedie più grandi) e Coriolano si successero a ritmo incalzante. E Dover Wilson si chiede: «Come fece Shakespeare a salvarsi l'anima, impegnato com'era in una delle imprese più pericolose e difficili mai intraprese dallo spirito umano?» Shakespeare sopravvisse; e sopravvisse solo per far seguire alle sue grandi tragedie quei drammi mirabili che sono Il racconto d'inverno e La tempesta.

Temo di essermi dilungato nel descrivere nei particolari la crescita dell'arte di Shakespeare. Desidero però sottolineare la grandezza di tale crescita. E sono certo che si possano dire cose simili sulle ultime composizioni di Beethoven, comprendenti le ultime cinque sonate per pianoforte, la Missa Solemnis e, soprattutto, gli ultimi cinque quartetti per archi.

Benché Shakespeare e Beethoven siano probabilmente unici nell'aver camminato sul filo del rasoio in prossimità della parte estrema della loro vita sopravvivendo a questa prova difficilissima, ci sono altri che illustrano, a un livello più modesto, la stessa costante ascesa sino a un culmine. Non conosco invece un solo scienziato per cui si possa dire la stessa cosa. (Sto escludendo il caso di coloro che, come Coates, Galois, Abel Ramanujan e Majorana, morirono giovani. Non sappiamo infatti quali risultati avrebbero potuto conseguire se fossero sopravvissuti a quella che, negli scienziati, è normalmente l'età più creativa.) In ogni caso, pare che gli scienziati, non siano in grado di sostenere un'ascesa costante e continua. Qual è la ragione di questo stato di cose? Io non tenterò di rispondere a questa domanda, ma passerò a qualche considerazione più concreta. La domanda che desidero affrontare ora è in che modo si possano valutare le teorie scientifiche come opere d'arte alla maniera della critica letteraria o della critica d'arte. Il caso della teoria generale della relatività ci fornisce un esempio, giacché quasi tutti sono d'accordo nel considerarla una bella teoria. Penso sia utile chiedersi quale sia la fonte di questa bellezza e credo che non rifiuterò una tale ricerca con un'asserzione come quella (fatta in un altro contesto) di Dirac:

«[La bellezza matematica] non può essere definita, come non può essere definita la bellezza nell'arte, ma le persone che studiano matematica di solito non hanno alcuna difficoltà ad apprezzarla».

Né penso che ci si dovrebbe accontentare di un'osservazione come quella di Born: «[La teoria generale della relatività] mi apparve come una grande opera d'arte, da godere e ammirare da lontano».

(Per inciso, posso dire, con tutta franchezza, che non so come considerare l'osservazione di Born? La teoria generale della relatività dev'essere ammirata solo da lontano? Non richiede forse di essere studiata e sviluppata come qualsiasi altra branca delle scienze fisiche?) Nonostante le difficoltà intrinseche che ostacolano discussioni come queste, io tenterò di chiarire perché la teoria generale della relatività piaccia al nostro senso estetico e perché la consideriamo bella. A questo scopo è necessaria adottare qualche criterio per la bellezza. Ne adotterò due. Il primo è il criterio di Francesco Bacone:

«Non c'è una bellezza eccellente che non abbia qualche stranezza nelle proporzioni!»

(Stranezza, in questo contesto, significa «eccezionalità a un grado tale da suscitare meraviglia e sorpresa».) Il secondo criterio, qual è formulato da Heisenberg, è complementare a quello di Bacone:

«La bellezza è l'appropriata conformità delle parti l'una all'altra e al tutto».

Che la teoria generale della relatività abbia qualche stranezza nelle proporzioni, nel senso baconiano, è chiaro. Essa consiste primariamente nel mettere in relazione, in giustapposizione, due concetti fondamentali che erano stati considerati fino allora del tutto indipendenti: i concetti di spazio e tempo, da un lato, e i concetti di materia e di moto dall'altro. In effetti, come scrisse nel 1919 Pauli: «La geometria dello spazio-tempo non è data; essa è determinata dalla materia e dal suo moto». Nella fusione di gravità e di metrica che ne seguì, Einstein compì nel 1915 ciò che Riemann aveva profetizzato nel 1854, ossia che il campo metrico dev'essere connesso in modo causale con la materia e il suo moto. Forse la maggiore stranezza nella proporzione consiste nell'alterazione che ne consegue nella nostra visione dello spazio e del tempo. Come scrisse Eddington: «Lo spazio non è una quantità di punti ravvicinati; è una quantità di distanze interconnesse».

C'è un altro aspetto nella fondazione della teoria generale della relatività da parte di Einstein che continua a meravigliarci. È questo: noi possiamo concedere facilmente che le leggi di gravitazione di Newton richiedano di essere modificate per tener conto del valore finito della velocità della luce e per rifiutare ogni azione a distanza istantanea. Con questa concessione ne segue che la deviazione delle orbite dei pianeti dalle predizioni newtoniane devono essere quadratiche in ν/c, dove ν è una misura della velocità del pianeta nella sua orbita e c è la velocità della luce. Nei sistemi planetari queste deviazioni, persino nei casi più favorevoli, possono ammontare a non più di poche parti per milione. Sarebbe stato perciò del tutto sufficiente se Einstein avesse cercato una teoria che tenesse conto di deviazioni di quell'entità minima dalle predizioni della teoria newtoniana per mezzo di un trattamento perturbativo. Quello non era però il modo di procedere di Einstein: egli cercò invece una teoria esatta, e pervenne alle sue equazioni di campo per mezzo di argomentazioni qualitative di natura fisica, combinate a un senso infallibile dell'eleganza e semplicità matematiche. Il fatto che Einstein sia riuscito a pervenire a una teoria fisica completa sulla base di un tale pensiero speculativo è la ragione per cui, quando seguiamo i suoi pensieri, abbiamo l'impressione che «un muro che ci separava dalla verità sia crollato» (Weyl).

Le osservazioni che precedono si applicano solo alle fondazioni della teoria che conducono alle equazioni di campo. Noi dobbiamo chiederci ora se, a un ulteriore esame, la teoria soddisfi il secondo criterio di bellezza, ossia «l'appropriata conformità delle parti l'una all'altra e al tutto». La teoria soddisfa abbondantemente questo criterio, rivelando al tempo stesso in ogni fase una «stranezza nelle proporzioni». Vorrei dare qualche esempio.

Consideriamo, innanzitutto, le soluzioni che la teoria generale della relatività consente per i buchi neri. Com'e noto, i buchi neri suddividono lo spazio tridimensionale in due regioni: una regione interna - limitata da una superficie bidimensionale liscia - di profondità nulla che è priva di comunicazioni con la regione esterna, la quale è, a sua volta, asintoticamente piana. È sorprendente che, con queste restrizioni molto semplici e necessarie, la teoria generale consenta, per buchi stazionari, una singola famiglia biparametrica di soluzioni. È questa la famiglia di Kerr, in cui i due parametri sono la massa e il momento angolare del buco nero. Quel che è ancora più notevole è che la metrica per questa famiglia di soluzioni è esplicitamente nota. La metrica di Kerr è asimmetrica e rappresenta un buco nero rotante sull'asse di simmetria.

Il carattere asimmetrico della geometria di Kerr garantisce chiaramente la conservazione dell'energia di una particella sperimentale che descrivesse una geodetica, oltre che di quella della sua componente del momento angolare attorno all'asse di simmetria. Oltre a queste due quantità conservate, la geometria di Kerr concede inaspettatamente alla particella sperimentale una terza quantità che si conserva (scoperta da Brandon Carter). Di conseguenza l'equazione di Hamilton­ Jacobi, che governa il moto di una particella sperimentale, è separabile nelle sue variabili; e la soluzione delle equazioni geodetiche può essere ridotta a quadrature. Questo fatto era alquanto sorprendente. Ma ancor più sorprendente è il fatto che tutte le equazioni della fisica matematica - l'equazione d'onda scalare, le equazioni di Maxwell, l'equazione di Dirac e le equazioni che governano la propagazione delle onde gravitazionali - sono tutte separabili nella geometria di Kerr (così come lo sono nella geometria di Minkowski) e possono quindi essere risolte esplicitamente.

Si prova uno stupore simile quando ci si rende conto che i teoremi della singolarità di Penrose e Hawking richiedono che il nostro universo debba necessariamente avere avuto origine in una singolarità e che, di conseguenza, noi siamo costretti a prendere in considerazione la natura dei processi fisici che si verificheranno a densità dell'ordine di 10⁹³ g/cm³ in volumi con dimensioni lineari dell'ordine di 10^-33 cm, e in intervalli di tempo dell'ordine di 10^-44 secondi, dimensioni che non possono non colpire persino questo pubblico.

O, di nuovo, il teorema di Hawking che l'area della superficie di un buco nero debba sempre aumentare suggerisce l'identificazione di tale area con l'entropia termodinamica del buco nero, e questa nozione conduce a un'intima connessione fra termodinamica, geometria e gravità.

In tutte queste cose non manca certamente la stranezza nelle proporzioni!

Tutto ciò che ho detto finora è conforme ai due criteri di bellezza da cui ho preso l'avvio. Ma c'è un altro aspetto ancora della natura che rimane da considerare.

Quando, una decina di anni fa, Henry Moore visito l'Università di Chicago, io ebbi occasione di chiedergli come si dovrebbero guardare le sculture: da lontano o da vicino? La risposta di Moore fu che le sculture più grandi possono - anzi dovrebbero - essere guardate da qualsiasi distanza giacché nuovi aspetti della bellezza si riveleranno a ogni scala.

Moore cita come esempi le sculture di Michelangelo. Nello stesso modo, la teoria generale della relatività rivela stranezza nelle proporzioni a qualsiasi livello si possano esplorare le sue conseguenze. Dobbiamo accontentarci di un esempio.

Se si ampliano le equazioni di Einstein nelle equazioni di Einstein-Maxwell, ossia nelle equazioni di campo appropriate a uno spazio pervaso da un campo elettromagnetico, e si cercano soluzioni dotate della simmetria sferica, si trova una soluzione che descrive un buco nero con una massa e una carica elettrica. Questa soluzione fu scoperta da Reissner e da Nordstrom come generalizzazione della ben nota soluzione di Schwarzschild. A causa della carica del buco nero è chiaro che, se esso viene investito da un'onda elettromagnetica, una certa frazione dell'energia elettromagnetica incidente sarà riflessa nella forma di onde gravitazionali. Inversamente, se il buco nero viene investito da un'onda gravitazionale, una certa frazione dell'energia gravitazionale incidente sarà riflessa nella forma di onde elettromagnetiche. Il fatto notevole è che le due frazioni sono identiche per tutte le frequenze. Questo risultato non era previsto; la causa sottostante è stata ora ricondotta alla reversibilità nel tempo delle leggi della fisica (classica). Questo esempio illustra come la stranezza nelle proporzioni si riveli nella teoria generale della relatività a ogni livello di esplorazione. Ed è questo fatto, più di qualsiasi altro, a contribuire alla bellezza senza pari della teoria generale della relatività.

Finora le mie osservazioni sono state limitate a quelle che tutti possiamo riconoscere come grandi idee concepite da uomini di grande genialità. Non ne segue, però, che la bellezza venga sperimentata solo nel contesto di grandi idee e da parte di uomini di grande genialità, così come non è vero che le gioie della creatività siano limitate a pochi fortunati. Esse sono, in effetti, accessibili a chiunque di noi, purché siamo sensibilizzati a percepire la stranezza nelle proporzioni e l'appropriata conformità delle parti l'una all'altra e al tutto. E si può provare soddisfazione anche dall'organizzare armonicamente un ambito della scienza con ordine, modello e coerenza. Esempi di un tale lavoro di organizzazione sono le Vorlesungen über Dynamik (Lezioni sulla dinamica) di Jacobi, le Vorlesungen über die Gastheorie (Lezioni sulla teoria dei gas) di Boltzmann, Atombau und Spektrallinien (Struttura dell'atomo e righe spettrali) di Sommerfeld, i Principi della meccanica quantistica di Dirac e i vari scritti preziosi composti da Schrodinger nei suoi ultimi anni. Lo splendore eterno che traluce attraverso i fenomeni materiali (per usare l'immagine di Plotino) illumina questi libri di uno sfavillio iridescente. Vorrei quindi concludere affermando che ciascuno di noi, ciascuno nel suo modo modesto, può ricavare soddisfazione nella propria ricerca della bellezza nella scienza, come i suonatori in The Waves (Le onde) di Virginia Woolf:

«C'è un quadrato, c'è un rettangolo. I suonatori prendono il quadrato e lo pongono sul rettangolo. Ve lo pongono sopra con molta cura; creano una dimora perfetta. Ben poco resta fuori. Ora la struttura è visibile; quanto c'è di rudimentale è qui dichiarato; noi non siamo così vari ne così meschini; abbiamo fatto rettangoli e li abbiamo collocati su quadrati. Questo è il nostro trionfo; questa è la nostra consolazione». [Virgina Woolf, Le onde, tr. it. di G. De Angelis, Rizzoli, Milano 1987, p.135]